
Cuando se necesita resolver un problema del mundo real es probable encontrar varias soluciones que permitan satisfacer las necesidades de éste. Por ello, también es probable encontrarse con un escenario en que haya soluciones más eficientes que otras y, en consecuencia, que su ejecución sea más rápida y sean mejores candidatas a ser desarrolladas e implementadas.
El análisis de algoritmos busca justamente resolver este escenario que se plantea determinando la eficiencia exacta de cada una de las posibles soluciones que puedan resolver el problema.
Tipos de complejidad
Cuando se habla de complejidad se hace referencia, casi todas las veces, a la complejidad temporal. No obstante, también existe otro tipo de complejidad: la espacial. La primera de ellas, determina de una forma exacta el tiempo (donde una posible unidad de medida son los segundos) de ejecución de un algoritmo. Sin embargo, la segunda de estas determina la cantidad de memoria utilizada (medida en bytes) por el algoritmo.
Entonces, ¿por qué cuando se habla de complejidad se hace referencia a la complejidad temporal y no a la espacial? La respuesta a esta pregunta la encontramos en la diferencia de costes que existe entre mejorar la capacidad de computación y la de almacenamiento. A día de hoy, es mucho más económico y rentable obtener más espacio en memoria que no mejorar la capacidad de cálculo de un computador. Es por eso que, cuando hay que decidir entre priorizar el espacio de memoria usado o el tiempo de ejecución según el tipo de algoritmo, se prioriza siempre utilizar más memoria para poder conseguir un tiempo de ejecución menor.
Forma de determinar su eficiencia
Una vez conocidos los dos tipos de complejidad existentes, hace falta conocer una forma única e inequívoca de poder determinar la complejidad para así poder comparar entre los diferentes algoritmos.
Antes, pero, es necesario precisar en base a qué se determinará la complejidad de un algoritmo y, concretamente depende de tres elementos: la cantidad de datos de entrada, el tipo de algoritmo que es y el computador que lo ejecuta.
El primero de todos se basa en la idea de que no es lo mismo tener que tratar una cantidad de datos pequeña como una cantidad muy grande. Por ejemplo, si hay que buscar un elemento entre un vector de 10 posiciones, en el peor de los casos solo habrá que recorrer 10 posiciones. Sin embargo, si el vector contiene 1000 posiciones, serán 1000. Por lo tanto, según la cantidad de datos de entrada el algoritmo tendrá una complejidad mayor o menor.
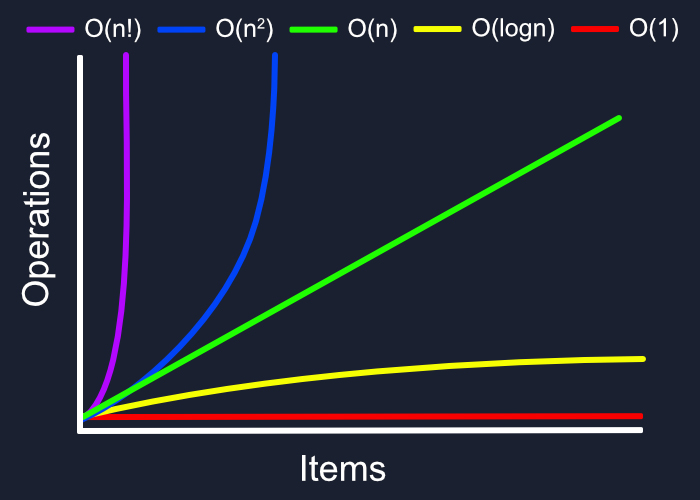
El segundo de ellos indica que un algoritmo tendrá mayor complejidad según las estructuras que tenga dentro. Por ejemplo, no es lo mismo ejecutar 10 líneas de código sin ninguna estructura iterativa dentro que hacerlo con un bucle donde esa cantidad de líneas se tendrá que ejecutar múltiples veces. Por lo tanto, según las estructuras que haya dentro del algoritmo, su complejidad será mayor o menor.
Finalmente, existe un último condicionante: el computador que lo ejecuta, ya que un mismo algoritmo con la misma cantidad de datos de entrada puede tardar más en un computador o en otro según los componentes que tenga. Además, también puede darse el caso que un algoritmo tarde un tiempo diferente en un mismo computador según el estado de este, ya que puede darse el caso en que ese computador esté usando gran parte del procesador en otra tarea y destine menos recursos a ejecutar el algoritmo. En cualquier caso, este elemento no suele tenerse mucho en cuenta a la hora de desarrollar un algoritmo, ya que en la mayoría de cosas, las diferencias sustanciales se encuentran en los dos primeros que se han explicado anteriormente.
Una vez definidos los elementos que determinan la complejidad, hay que tener en cuenta que un mismo algoritmo puede ejecutar diferente parte del código con estructuras condicionales o, incluso, no iterar siempre las mismas veces una estructura iterativa. Entonces, es necesario hablar de lo que se conoce como el peor caso. Este determina la situación en que se tendrán que ejecutar más líneas de código (o repetir más veces una estructura iterativa) y es el escenario en base a lo que se debe determinar la complejidad de un algoritmo.
Pero, ¿por qué hay que tener en cuenta este escenario para determinar su complejidad? La realidad es que, como ya se ha dicho, no siempre se ejecutarán la misma cantidad de líneas de un mismo algoritmo, como tampoco se van a tener que recorrer la misma cantidad de elementos de un vector en una búsqueda. Por ejemplo, si se parte del vector {1, 2, 3, 4, 5} y se busca el elemento con valor 1, parece claro que lo encontrará en la primera posición y no tendrá que seguir buscando. No obstante, esto es solo un caso concreto y, en la gran mayoría de los casos, el algoritmo no encontrará el valor deseado en la primera posición del vector.
Por lo tanto, es necesario generalizar este raciocinio para poder determinar la complejidad que tendrá un algoritmo en la mayoría de los casos. Siguiendo con el ejemplo propuesto, esta situación se dará cuando el elemento buscado no se encuentre dentro del vector, puesto que, en una situación real, será un caso bastante recurrente. Así pues, siempre que se quiera determinar la complejidad de un algoritmo, se tendrá que tener en cuenta el peor caso: que recorra todas las posiciones de un vector, que siempre se ejecuten los bloques condicionales de mayor complejidad, etc.
De este modo, habiendo citado todas las consideraciones previas, ya se puede empezar a determinar la complejidad temporal de forma exacta. Para ello, se establece un criterio donde se asigna una cantidad de tiempo a cada operación elemental que se realiza. De este modo, la suma de todas ellas determinará la complejidad temporal total.
En este caso, para facilitar el cálculo de la complejidad siempre se determina que todas las operaciones llamadas elementales tardan la misma cantidad de tiempo en ser ejecutadas. Normalmente, se suelen determinar con una constante, por ejemplo, kx (donde x es un número natural). Las llamadas operaciones básicas son: sumas, restas, multiplicaciones, divisiones, módulos, incrementos de variables (con la operación ++ o --), comparaciones (todo tipo de comparaciones lógicas -mayor que, menor que, igual que, negaciones, puertas lógicas AND y OR, etc.-) y asignaciones.
Una vez determinado el coste temporal, habrá que agrupar las operaciones en las constantes que se han citado según la estructura en la cual estén. Para ello, si hay un bucle en el algoritmo, se intentará agrupar todas las operaciones elementales en una única constante que se ejecutará tantas veces como el bucle se itere. Es decir, si el bucle se ejecuta n veces, el valor de la constante k se tendrá que multiplicar por n. Finalmente, para enlazar las constantes de diferentes estructuras, si estas se encuentran al mismo nivel y se ejecutan independientemente, solo habrá que sumar ambas complejidades.
Por otro lado, la complejidad espacial también puede ser medida con exactitud, más no resultará tan interesante y determinante como la temporal. Para ello, habrá que medir la cantidad de bytes que ocupan todas las variables (ya sean variables primitivas del lenguaje o estructuras abstractas) y, la suma de ellas, será el espacio en memoria que utilizará ese algoritmo.
La eficiencia de los algoritmos
En caso de tener un vector ordenado de elementos donde se quiera buscar en qué posición se encuentra cierto valor, existen múltiples formas de obtenerlo. Para este ejemplo, se buscará determinar qué método es más eficiente para dicho problema: una búsqueda secuencial o una búsqueda binaria (también conocida como dicotómica).
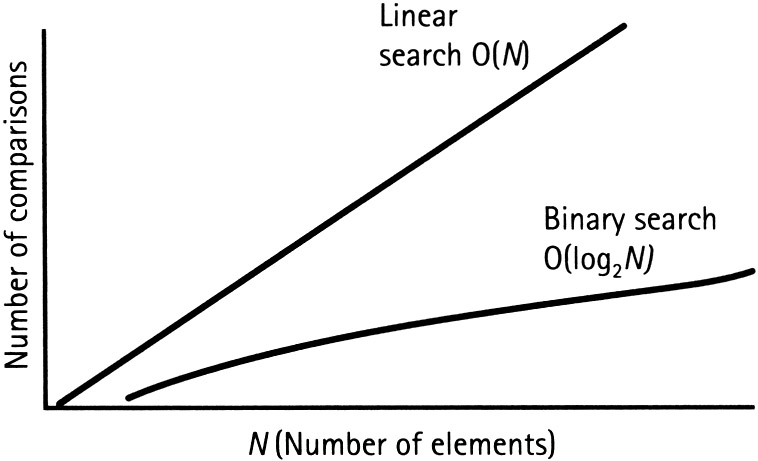
Por un lado, la búsqueda secuencial empezará por el inicio o por el final de la lista e irá incrementando o decrementando el índice en el cual va a comprobar si es el valor que está buscando. El elemento a buscar puede que se encuentre en la primera posición, pero también puede ser que esté en medio, al final o que directamente no esté. Entonces, ¿cuál será la complejidad de ese algoritmo? Es decir, ¿qué cantidad de recursos va a necesitar dicho algoritmo para encontrar el valor deseado?
Parece evidente que la cantidad de tiempo de ejecución no va a ser el mismo si se encuentra en la primera posición o en la última. Por ello, hay que determinar un escenario que sea igual para todos los métodos de búsqueda en este caso y que permita dictaminar la cantidad de tiempo máximo que estará en ejecución. Justamente eso es lo que se conoce como el peor caso. Es necesario valorar siempre la eficiencia de un algoritmo en función de este, ya que no tiene sentido valorarla en función de si el elemento está en la primera posición o en el medio, ya que no serán las situaciones más comunes y nada garantiza que el elemento a buscar esté realmente en la lista. Debido a esto, siempre se va a valorar la eficiencia de un algoritmo en función del peor caso y, en el caso del ejemplo, es que el valor buscado no se encuentre en la lista.
Por otro lado, la búsqueda binaria o dicotómica empezará su búsqueda por el valor central de la lista e irá descartando mitades. Realizará tal operación de forma iterativa hasta encontrar el valor o determinar que el valor a buscar no se encuentra en la lista. Con lo cual, este método de búsqueda no tendrá que buscar entre todos los elementos de la lista, sino que irá descartando mitades de forma recursiva hasta finalizar. En consecuencia, tardará menos tiempo en ejecutarse y su complejidad es logarítmica: O (log n). No obstante, para verificarlo, es necesario formalizarlo.
En conclusión, en el primer caso, el de la búsqueda secuencial, accedería a todos los elementos de la lista. Suponiendo que la cantidad de elementos sea n, tendría n iteraciones. Formalmente, se puede expresar en notación asintótica de la siguiente manera: O(n).
Ejemplo práctico
Para realizar un ejemplo, se partirá del siguiente algoritmo:
int getModulesCount(int numbers[], int size, int search)
{
int count;
count = 0;
for (int i = 0; i < size; i++)
{
if (numbers[i] % search == 0)
count++;
}
return count;
}
Siguiendo las indicaciones que se han dado en los párrafos anteriores, se puede observar que este algoritmo tiene dos partes claramente diferenciadas: la línea que hay antes del bucle for y el propio for. Por lo tanto, se tendrá que determinar un valor para la complejidad de esa primera parte y, otra, para la segunda.
En el caso de línea 3, aparece una operación elemental (una asignación) a la cual se le asignará la constante k1 para indicar el valor de su complejidad.
Por otro lado, desde la línea 7 hasta la 11, aparecen varias operaciones elementales juntamente con un bloque condicional. Por lo tanto, se podrán agrupar todas esas operaciones en otra constante que se va a llamar k2. Además, hay que tener en cuenta que el peor caso de este algoritmo es que siempre se cumpla la condición del bloque condicional de la línea 9 y, consecuentemente, ejecute el código de la línea 10. Asimismo, todo este bloque del algoritmo se ejecutará la cantidad de veces cuyo valor tenga la variable size. En este caso, se le va a llamar n.
Concretamente, el valor de k2 es la suma de las siguientes operaciones elementales: la asignación sobre la variable i del for, la comparación que tiene el for, el incrementador de la variable i que tiene el for, la operación módulo del bloque condicional if, la comparación del mismo bloque condicional y, finalmente, el incremento de la variable count. Todas ellas hacen una suma de 6 operaciones elementales. Así, el valor de k2 es de 6 operaciones elementales.
Finalmente, una vez determinado el valor exacto de cada una de las constantes y habiendo analizado las estructuras que aparecen en el algoritmo se concluye que la ecuación que determina la complejidad temporal de este bloque de código és:
De este modo, se puede observar como existe una dependencia de la cantidad de datos que entran al algoritmo (mediante la variable size que se ha representado como n en esta ecuación. En este caso, la dependencia es de solo un grado, por lo tanto, se concluye que la complejidad será lineal. En notación asintótica, o de big O en inglés, se expresa como O (n).
Conclusión
Mediante el análisis de algoritmos se puede determinar la complejidad de cada uno de ellos, es decir, el tiempo de ejecución que tendrá ese programa en función de la cantidad de datos de entrada. En situaciones reales este análisis permitirá elegir justificadamente un algoritmo u otro para ser desarrollado e implementar la solución más eficiente a un problema real.
Más información
Si te ha gustado este artículo, te proponemos unos enlaces con los que profundizar sobre la idea del análisis de algoritmos. Además, si quieres una explicación más detallada y con muchos más ejemplos, te aconsejamos el vídeo del curso de Prácticas de programación donde se analiza completamente.
- Análisis de algoritmos paso a paso: cómo analizar un algoritmo.
- Tipos de complejidad: complejidades según la cantidad de datos de entrada.
- Complejidad de TAD: complejidad de los métodos de los TAD.
Si consideras que hay algún error en este artículo háznoslo saber mediante nuestro correo [email protected].
